Posts Forecasting at Scale总结
Post
Cancel

Forecasting at Scale总结

dazuo Jul 2, 2020 2020-07-02T20:19:00+08:00
Nov 6, 2022 2022-11-06T19:54:18+08:00 14 min

原文链接： Forecasting at scale

引言

时间序列预测的难点

  • 通常的预测算法无法融入专家的经验和假设
  • 算法调试难度大
  • 时间序列预测领域的专业人才比较稀缺

希望解决的问题

  • 降低算法门槛
  • 适用于各种不同类型的预测问题
  • 全自动产生大量序列的预测结果
  • 可以将专家经验结合到预估算法中

商业时间序列的特点

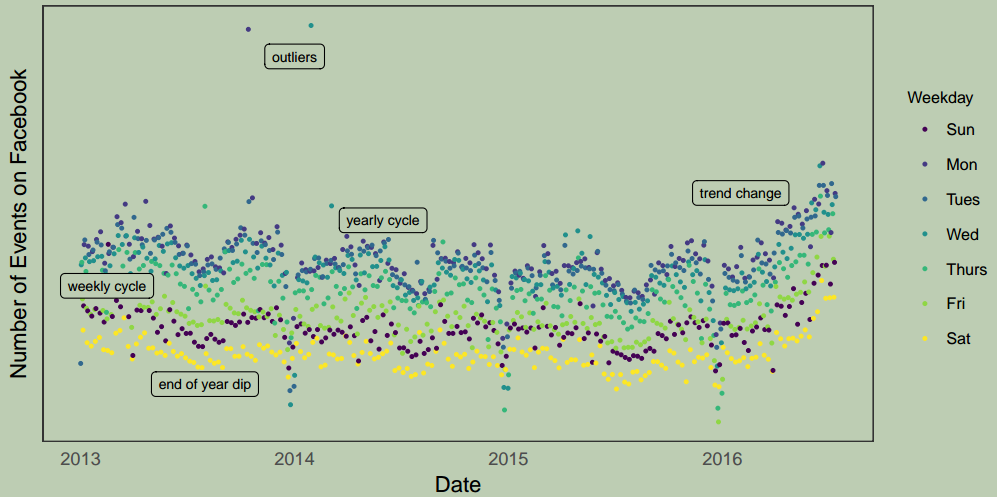image-20220826202014707图2: Facebook上创建的事件数。每一天对应一个点，点按周的天数进行颜色编码，以显示周周期。该时间序列的特征代表了许多商业时间序列：多重强季节性、趋势变化、异常值和假日效应。

四个组成分量

  • Trend

    较长一段时间内呈现出来的持续向上或持续向下的变动。

  • Seasonality

    周期性/季节性。通常以日、周、年为单位的周期性变化。

  • Regressor

    外部变量。已知的、引起短期波动的因素，如节假日、促销等。

  • Noise

    残差。由未知因素产生的波动。如果产生因素知道了，就变成了外部变量。

传统时间序列预测方法的缺陷

传统时间序列预测方法都是自回归模型(Auto Regression): \(y_{t}=f(y_{t-1}, y_{t-2}, ..., y_{t-n})\) 自回归的理解：输入是观测变量的历史值，输出是观测变量的未来值，相当于观测值自己对自己的回归。

比如移动平均模型： \(y_{t} = \sum_{i=1}^{n}w_{i}y_{t-i}\) 难以理解，难以调试。

Prophet模型原理

\(y(t) = g(t) + s(t) + h(t) + \epsilon_{t}\) 这里：

  • $g(t)$ 是趋势函数，用于模拟时间序列值的非周期性变化。用分段线性函数或者logistic函数拟合。
  • $s(t)$ 表示周期性变化（例如，每周和每年的季节性）。用傅里叶级数拟合。
  • $h(t)$ 代表在一天或几天内可能出现的不规则日程上的假日影响。用线性函数拟合。
  • 误差项 $\epsilon_{t}$ 表示模型不适应的任何特殊变化；稍后，我们将假设 $\epsilon_{t}$ 服从正态分布。

logistic增长曲线

\[g(t) = \frac{C}{1+\text{exp}(-k(t-m))}\]

image-20220826202014707

以下超参数，由用户给定:

  • $C$，carrying capactity，曲线的渐近线。当 $k>0$ 时，其表示曲线的上限；当 $k<0$ 时，其表示曲线的下限。

以下参数，由训练得到:

  • $k$，增长速率。当 $k>0$ 时，曲线呈上升趋势；当 $k<0$ 时，曲线呈下降趋势。
  • $m$，曲线拐点对应的时间，即上图中红线和蓝线的分界点。

分段logistic增长曲线

假设增长曲线在 $S_{j}, j=1,…,s$ 时刻发生了变化(分段点) ，增长速率变化量为 $\delta_{j}$ ，拐点的变化量为 $\gamma_{j}$，那么在 $t \in [S_{j}, S_{j+1})$ 时刻，

增长速率为 $k+ \sum_{l \le j} \delta_{l}$ ；拐点为 $m+ \sum_{l \le j} \gamma_{l}$

写成向量形式：$k + \pmb{a}(t)^{\top} \pmb{δ}$ ；$m + \pmb{a}(t)^{\top} \pmb{\gamma}$

其中， $a_{j}(t) = \begin{cases} 1 &\text{if} \ t \ge s_{j}
0 &\text{otherwise} \end{cases}$

所以，分段logistic增长曲线可以写成： \(g(t) = \frac {C(t)} { 1 + \text{exp}( -(k+ \pmb{a}(t)^{\top} \pmb{\delta}) (t-(m+\pmb{a}(t)^{\top} \pmb{\gamma})) ) }\) 为了保证 $g$ 的连续性： \(\gamma_{j} = \Big(s_{j} -m - \sum_{l < j} \gamma_{l} \Big) \Big(1 - \frac{k + \sum_{l<j} \delta_{l}}{k+\sum_{l \le j} \delta_{l}} \Big)\) 以下超参数，由用户给定:

  • $C(t)$，曲线的渐近线。

  • n_change_points，分段点的数量。

  • $b$，$\delta$ 的先验概率分布。假设 $\delta$ 满足均值为0，标准差为 $b$ 的拉普拉斯分布。

    $b$ 越大，增长波动越大，越容易过拟合；$b$ 越小，增长波动越小，越容易欠拟合。

以下超参数，可由用户给定，也可由训练得到:

  • $S_{j}$，分段点的位置。如果用户指定了 $S_{j}$ ，那么n_change_points不会起作用。

以下参数，由训练得到:

  • $k$，第一段曲线的增长速率
  • $m$，第一段曲线的拐点
  • $\delta_{j}$，增长速率的变化量

线性趋势函数和分段线性趋势函数

线性趋势函数 \(g(t) = kt + m\) 分段线性趋势函数 \(g(t) = (k+ \pmb{a}(t)^{\top} \pmb{\delta})t + (m+ \pmb{a}(t)^{\top} \pmb{\gamma})\) 以下超参数，由用户给定:

  • n_change_points，分段点的数量。
  • $b$，$\delta$ 的先验概率分布。

以下超参数，可由用户给定，也可由训练得到:

  • $S_{j}$，分段点的位置。如果用户指定了 $S_{j}$ ，那么n_change_points不会起作用。

以下参数，由训练得到:

  • $k$，第一段曲线的增长速率
  • $m$，第一段曲线的拐点
  • $\delta_{j}$，增长速率的变化量

Prophet 可以计算趋势的置信区间

根据历史数据中分段点发生的频率和增长率的平均变化幅度，估计未来的时间点分段点发生的概率和变化幅度的分布：

$\lambda = \frac{1}{S} \sum_{j=1}^{S} \vert \delta_{j} \vert$

$\forall j>T, \quad \begin{cases} \delta_{j}=0 &\text{w.p.} \ \frac{T-S}{T}
\delta_{j} \sim \text{Laplace}(0, \lambda) &\text{w.p.} \ \frac{S}{T} \end{cases}$

根据以上假设，模拟多个可能的未来趋势线，从而计算趋势的不确定性。

哪些专家知识可以整合在趋势曲线里

  • 选择 线性 还是 logstic趋势线
  • 趋势的上下限(仅针对logstic趋势线，通过调整超参数 $C$ )
  • 指定分段点的数量和位置(通过调整超参数 $S_{j}$ )
  • 趋势线的波动程度(通过调整超参数 $b$ )

用傅里叶级数拟合季节性

任何周期性函数都可以表示成傅里叶级数 \(s(t) = \sum_{n=1}^{N} \Big(a_{n} \text{cos} \Big(\frac{2\pi nt}{P} \Big) + b_{n} \text{sin} \Big(\frac{2\pi nt}{P} \Big) \Big)\)

以下超参数，由用户给定：

  • $P$，周期长度
  • $N$，傅里叶级数的阶数。$N$ 越大，季节性曲线波动越大，越容易过拟合。
  • $\sigma$ ，$a_{n}, b_{n}$ 的先验概率分布。假设 $a_{n}, b_{n}$ 均值为0，标准差为 $\sigma$ 的正态分布。$\sigma$ 越大，季节性曲线波动越大，越容易过拟合。

以下参数，由训练得到：

  • $a_{n}, b_{n}$，傅里叶级数的系数。

哪些专家知识可以整合在季节性曲线里

  • 周期长度
  • 季节性曲线的波动大小（通过调整超参 $N$ 和 $\sigma$ ）

外部因素的影响

\[h(t) = Z(t)\pmb{\kappa}\]

其中，$Z(t) = [\pmb{1}(t \in D_{1}),…,\pmb{1}(t \in D_{L})]$，模型输入，外部因素在 $t$ 时刻的取值

$\pmb{\kappa}$ 为线性回归系数。

以下超参数，由用户给定：

  • $\nu$ ，$\kappa$ 的先验概率分布。假设 $\kappa$ 服从均值为0，标准差为 $\nu$ 的正态分布。$\nu$ 越大，外部因素对结果的影响越大，越容易引起过拟合。

以下参数，由训练得到：

  • $\kappa$，线性回归系数。

哪些专家知识可以整合在外部变量的曲线里

  • 需要加入哪些外部变量
  • 外部变量在每个时间点的取值
  • 外部因素对结果的影响的可能性大小（通过调整超参数 $\nu$ ）

Prophet模型优势

  • 可以灵活调整趋势、周期性的函数形式
  • 不需要对历史数据中的缺失值、异常值进行填补。因为是把历史数据中的一个时间点的数据作为训练样本，如果这个时间点缺失值、异常值，不把其放进训练数据集即可。
  • 拟合速度快。
  • 预测结果具有高度的可解释性和可调整性。因为模型本身分成了4个分量，可以针对每个分量进行分析。

Prophet模型缺点

  • 难以体现外部因素的非线性性

    比如，已知夹克的销量对温度很敏感。用Prophet预测夹克销量时，如何考虑温度的影响？

    温度对夹克销量的影响是非线性的，因为温度很低或者很高时，人们对夹克的需求都很小。所以很难用Prophet拟合温度对夹克销量的影响。

    有经验的专家可以先找到温度对夹克影响的拐点，然后用分段线性曲线去拟合。

  • 难以用于历史数据较短的序列

    已知冰激凌的销量具有很强的yearly周期性。假设有一款冰激凌是今年5月份新上市的，能否根据它在5月份的销量，用Prophet准确预测它在6、7月份的销量？

    对于新款冰激凌，历史数据过少，Prophet无法拟合出季节性，所以很难预测在6、7月份的销量。

    有经验的专家可以先用Prophet拟合近似的老产品的季节性，在将该季节性作为新款冰激凌预测时的外部变量。

预测模型自动评估通用方案

  • 用一个尽可能简单的方法设置预估效果的基准线
  • 确定用于评价模型精度的指标
  • 模拟模型在历史数据中的表现
  • 从误差分析模型优化的机会点

常见的预估模型精度评价指标

MAD/MAE

Mean Absolute Deviation or Mean Absolute Error \(MAD=\frac{1}{n} \sum_{t=1}^{n} \vert a_{t} - f_{t} \vert\)

MAPE

Mean Absolute Percentage Error \(MAPE=\frac{1}{n} \sum_{t=1}^{n} \vert \frac{a_{t} - f_{t}}{a_{t}} \vert\)

WMAPE

Weighted MAPE

最常见，有时也会被称作MAPE。 \(WMAPE = \frac{ \sum_{t=1}^{n} \vert a_{t} - f_{t} \vert} {\sum_{t=1}^{n} a_{t}}\)

模拟模型在历史数据中的表现

不能用交叉验证模拟模型的效果。

正确做法：back test

用滑动窗口的循环产生训练集和测试集。

image-20220826202014707

Prophet

  • 创建Prophet的实例
  • 对历史数据调用fit方法
  • 调用predict方法

Prophet的输入是一个dataframe，dataframe有2列：ds和y

  • ds(date stamp)，Pandas期望的格式YYYY-MM-DD或YYYY-MM-DD HH:MM:SS
  • y，数值
时间序列预测
Forecasting at Scale
This post is licensed under CC BY 4.0 by the author.
Recent Update
Contents

Forecasting at Scale

三、程序的机器级表示