这是一门非常优秀的OpenMP入门教程,讲解人Tim Mattson也曾参与过OpenMP的开发。
1. 概述
课程是简洁的lectures + 简短的execises的方式,讲究边学边练边掌握。
课程由五大模块组成,每个模块由一系列单元和讨论组成:
Getting Started with OpenMPThe Core Features of OpenMPWorking with OpenMPAdvanced OpenMP TopicsRecapitulation
总共27个lecture。
2. 并行编程介绍-1
摩尔定律说集成电路上可容纳的晶体管数量大约每18个月便会增加一倍。芯片上更多的晶体管数量带来了更优秀的性能,作者认为以前程序的性能来自于芯片硬件。你可以随心所欲的写你的软件,不用考虑性能,把性能留给了芯片硬件。更先进(晶体管数量更多)的芯片,更优秀的性能。
但是有一点不得不考虑,那就是功耗。根据Intel的研究,功耗和性能有这样一个拟合关系$power=perf^{1.74}$。
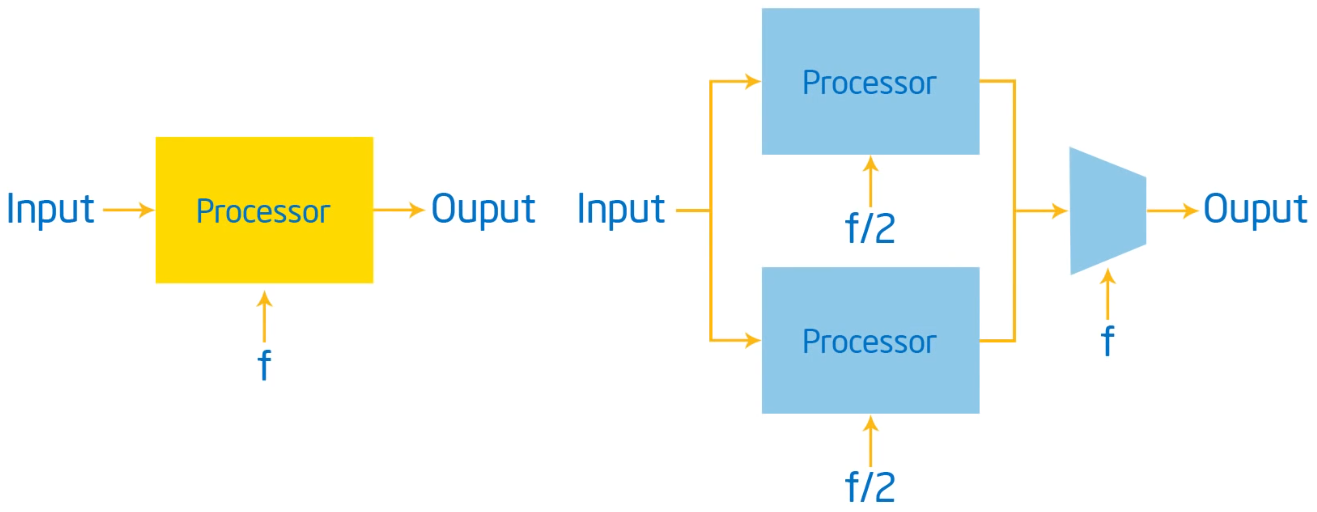
| 单核架构 | 多核架构 |
|---|---|
| Capacitance = C Voltage = V Frequency = F Power = $CV^{2F}$ | Capacitance = 2.2C Voltage = 0.6V Frequency = 0.5F Power = $0.396CV^{2F}$ |
对比可以看出多核架构使我们能够以更低的频率完成相同的工作,同时节省大量的功耗。
3. 并行编程介绍-2
并发 vs. 并行
| 并发 | 并行 |
|---|---|
| 系统中多个任务同时在逻辑上处于活动状态 | 系统中多个任务同时在实际上处于活动状态 |
| 并发应用 | 并行应用 |
|---|---|
| 根据应用的语义,计算在逻辑上同时执行的一种应用程序。 这个问题基本上是同时发生的。 | 一种应用程序,其计算实际上是同时执行的 以便在更短的时间内计算问题 问题本身可以串行描述,并不需要并发性。 |
OpenMP
- 用于编写多线程应用的
API。 - 为并行应用程序员提供的一组编译器指令和库方法。
- 极大简化了
Fortran,C/C++多线程程序的编写。
OpenMP解决方案栈
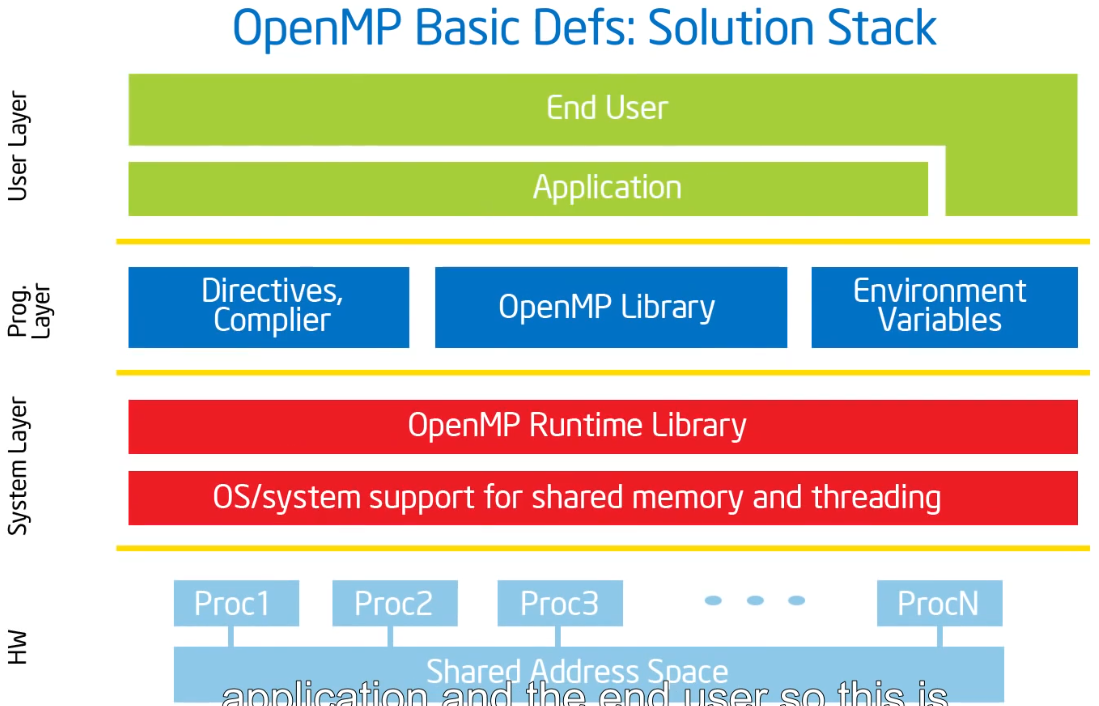
OpenMP核心语法
- OpenMP中大部分constructs是compiler directives.
#pragma omp construct [clause [clause]...]#pragma omp parallel num_threads(4)#include <omp.h>- 大部分
OpenMPconstructs作用于Structured Block. Structured Block: 一个或多个语句块,顶部有一个入口点,底部有一个出口点。
4. 使用OpenMP编译(Hello World)
1
2
3
4
5
gcc -fopenmp foo.c
export OMP_NUM_THREADS=4
./a.out
Exercise 1
Verify that your OMP environment works, write a multithreaded program that prints “Hello World”.
5. 讨论1-Hello World、线程如何工作的
1
2
3
4
5
6
7
8
9
10
11
12
13
#include <stdio.h>
#include <omp.h>
int main()
{
#pragma omp parallel
{
int ID = omp_get_thread_num();
printf("hello(%d)", ID);
printf(" world(%d) \n", ID);
return 0;
}
}
#pragma omp parallel 申请默认数量的线程。 omp_get_thread_num() 返回每个线程的唯一标识。范围是[0,N]。
共享内存计算机
任何由共享一份地址空间的多个处理单元组成的计算机。有两类:
对称多处理器(
SMP)一个共享地址空间,每个处理器访问地址空间的时间消耗是相同的,操作系统以相同的方式处理每个处理器。
非统一地址空间多处理器(
NUMA)不同的内存区域具有不同的访问成本。想像将内存分为“近”内存和“远”内存。
OpenMP概览
- OpenMP是一种多线程共享地址模型。
- 线程间通过共享变量进行通信。
- 意外共享数据会导致竞争状况。
- 竞争条件:当程序的结果随着线程调度的不同而改变时。
- 要控制竞争条件,请使用同步来保护数据冲突。
- 同步是昂贵的。
6. 创建线程(Pi程序)
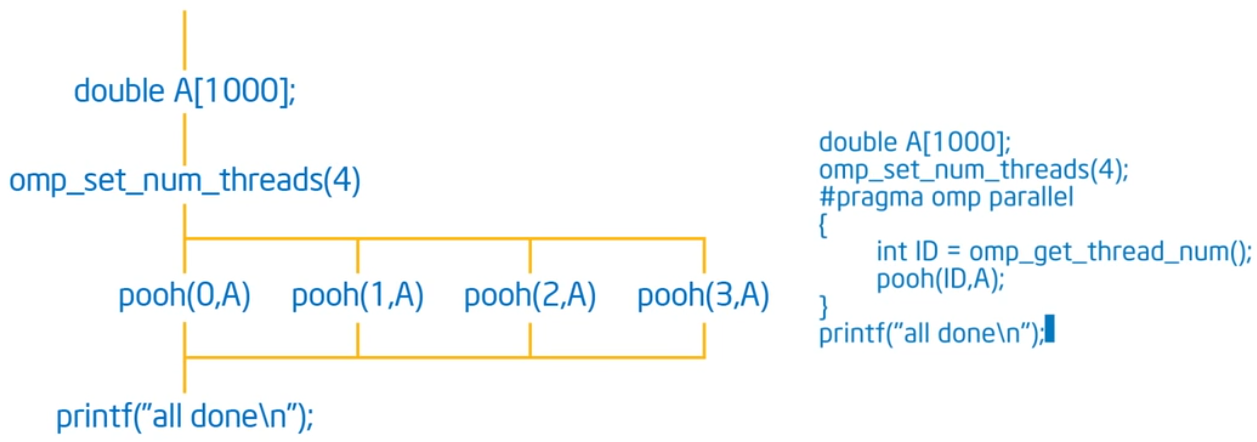
fork-join并行
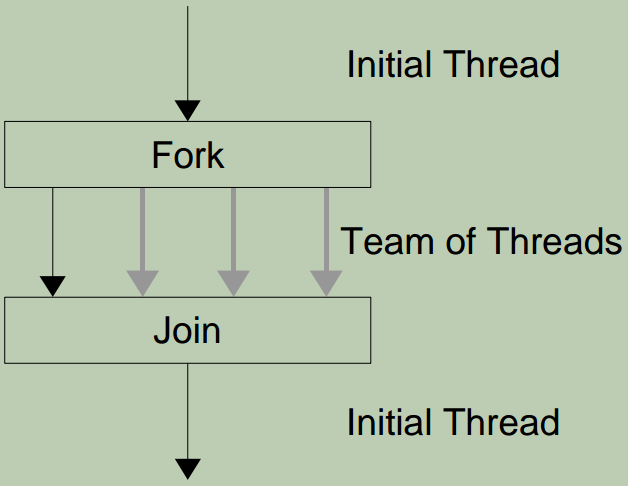
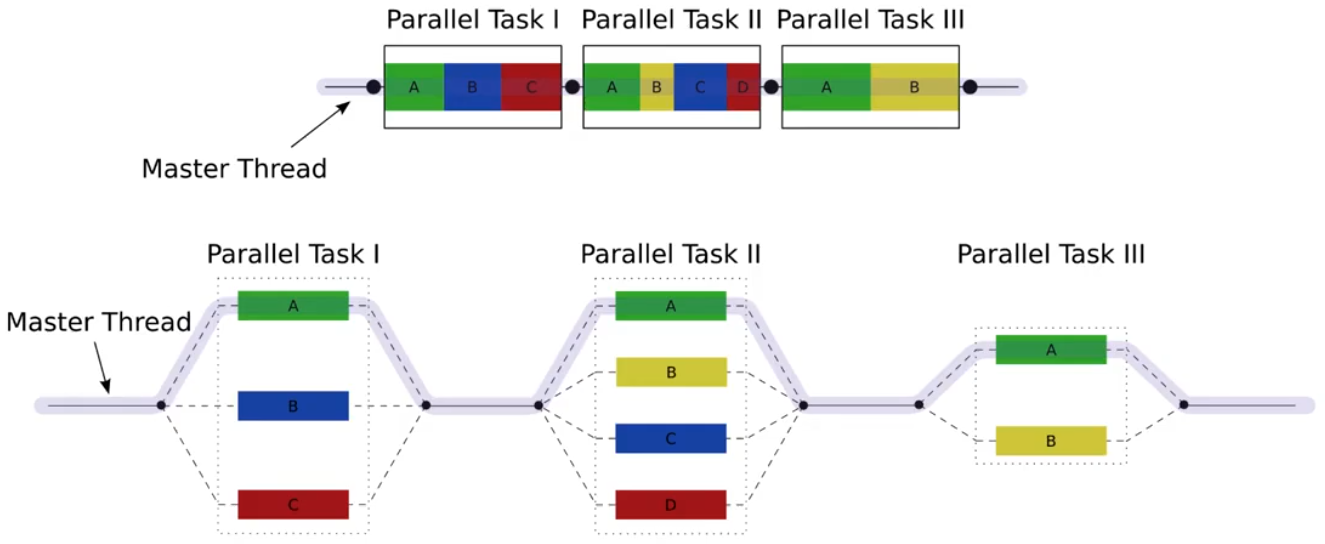
在某个时刻fork若干个线程,在另外某个时刻join到一起。下面是一个简单的例子:
Exercise 2
把下面这个串行版本的计算Pi值的程序改成并行版本。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void calc_pi_serial()
{
long num_steps = 0x20000000;
double sum = 0.0;
double step = 1.0 / (double)num_steps;
double start = omp_get_wtime( );
for (long i = 0; i < num_steps; i++) {
double x = (i + 0.5) * step;
sum += 4.0 / (1.0 + x * x);
}
double pi = sum * step;
printf("pi: %.16g in %.16g secs\n", pi, omp_get_wtime() - start);
// will print "pi: 3.141592653589428 in 5.664520263002487 secs"
}
7. 讨论 2-简单的Pi程序及为什么性能如此差
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#define NUM_THREADS 2
void calc_pi_omp_v1()
{
long num_steps = 0x20000000;
double sum[NUM_THREADS] = { 0.0 };
double step = 1.0 / (double)num_steps;
int nthreads;
double start = omp_get_wtime( );
omp_set_num_threads(NUM_THREADS);
#pragma omp parallel
{
int id = omp_get_thread_num();
int nthrds = omp_get_num_threads();
if (id == 0) { // master thread
nthreads = nthrds;
}
for (long i = id; i < num_steps; i += nthrds) {
double x = (i + 0.5) * step;
sum[id] += 4.0 / (1.0 + x * x);
}
}
double pi = 0;
for (int i = 0; i < nthreads; i++) {
pi += sum[i]*step;
}
printf("pi: %.16g in %.16g secs\n", pi, omp_get_wtime() - start);
}
上述并行版本可以得到正确的结果,但是当NUM_THREADS的值配置的更大的时候,耗时反而增加了。
原因是伪共享(false sharing)。
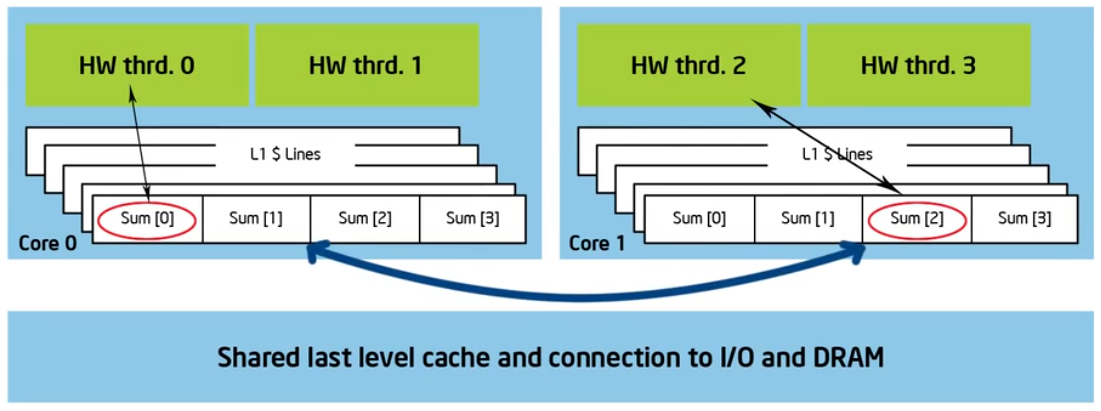
伪共享
If independent data elements happen to sit on the same cache line, each update will cause the cache lines to “slosh back and forth” between threads.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#define NUM_THREADS 4
#define PAD 8 // assume 64 byte L1 cache line size
void calc_pi_omp_v1()
{
long num_steps = 0x20000000;
double sum[NUM_THREADS][PAD] = { 0.0 };
double step = 1.0 / (double)num_steps;
int nthreads;
double start = omp_get_wtime( );
omp_set_num_threads(NUM_THREADS);
#pragma omp parallel
{
int id = omp_get_thread_num();
int nthrds = omp_get_num_threads();
if (id == 0) {
nthreads = nthrds;
}
for (long i = id; i < num_steps; i += nthrds) {
double x = (i + 0.5) * step;
sum[id][0] += 4.0 / (1.0 + x * x);
}
}
double pi = 0;
for (int i = 0; i < nthreads; i++) {
pi += sum[i][0]*step;
}
printf("pi: %.16g in %.16g secs\n", pi, omp_get_wtime() - start);
}
上述解决方案中通过增加[PAD]这一维,来保证sum[nthreads]中连续的元素存在于不同的cache line上。
8. 同步(再看Pi程序)
- OpenMP是一种多线程共享地址模型。
- 理解共享数据会导致竞争状况。
- 要控制竞争条件,请使用同步来保护数据冲突。
- 改变数据的访问方式来最小化对同步的需求。
高层同步:
critical(Mutual exclusion)atomicbarrierordered
底层同步:
flushlocks(both simple and nested)
critical原语
在某一时刻,只有1个线程会执行critical 块,不会有多个线程同时执行。
1
2
3
4
5
6
7
8
9
10
11
12
13
float res;
#pragma omp parallel
{
float B; int id, nthrds;
id = omp_get_thread_num();
nthrds = omp_get_num_threads();
for (int i = id, i < niters; i += nthrds) {
B = big_job(i);
#pragma omp critical
res += consume(B);
}
}
atomic原语
atomic里的语句只能是下列形式中的一种。
1
2
3
4
5
6
7
x binop = expr
x++
++x
x--
--x
x is an lvalue of scalar type and binop is a non-overloaded built in operator.
1
2
3
4
5
6
7
8
9
#pragma omp parallel
{
double tmp, B;
B = DOIT();
tmp = big_ugly(B);
#pragma omp atomic
X += tmp;
}
Exercise 3
修改Exercise 2中的代码,来解决由于sum数组引入的false sharing问题。
9. 讨论3-同步的开销和消除伪共享
在7的解决方案中,通过增加[PAD]这一维,来保证sum[nthreads]中连续的元素存在于不同的cache line上,从而消除了伪共享。
但是cache line的size在不同机器上可能不一样,7的解决方案就不具有可移植性,并且不够优雅。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
void calc_pi_omp_v2()
{
long num_steps = 0x20000000;
double step = 1.0 / (double)num_steps;
int nthreads;
double start = omp_get_wtime( );
double pi = 0.0;
omp_set_num_threads(NUM_THREADS);
#pragma omp parallel
{
// sum需要是线程私有的,不能放在并行域外,否则结果不正确,切耗时更长
double sum;
long i;
int id = omp_get_thread_num();
int nthrds = omp_get_num_threads();
if (id == 0) {
nthreads = nthrds;
}
for (i = id, sum = 0.0; i < num_steps; i += nthrds) {
double x = (i + 0.5) * step;
sum += 4.0 / (1.0 + x * x);
}
#pragma omp critical
pi += sum * step;
/*// 下面这3行的写法跟上面2行的效果类似
sum *= step;
#pragma omp atomic
pi += sum;
*/
}
printf("pi: %.16g in %.16g secs\n", pi, omp_get_wtime() - start);
}
10. 并行化循环(让Pi程序简单)-1
Worksharing
- Loop Construct
- Sections/Section Construct
- Single Construct
- Task Construct
Loop Worksharing Construct
Schedule Clause
schedule子句影响循环迭代映射到线程的方式。
schedule(static [, chunk]): 迭代空间被划分为chunk大小的块,块以round-robin方式分配给线程。若未指定块:#线程块。schedule(dynamic [, chunk]): 迭代空间分为chunk大小(未指定:1)的块,块按线程完成之前块的顺序调度到线程。schedule(guided [, chunk]): 与动态相似,但块大小从实现定义的值开始,然后以指数形式减小到块。schedule(runtime): 从OMP_SCHEDULE环境变量(或运行时库)获取调度和块大小。schedule(auto): 调度策略在运行时选择(不必是上述任何一项)。
何时使用schedule clause
static由程序员预先确定。在编译时完成调度,运行时的工作量最小。
dynamic每次迭代的工作都是不可预测的、高度可变的。运行时的工作量最大。运行时使用复杂调度逻辑。
11. 并行化循环(让Pi程序简单)-2
- 找到compute-intensive的for循环
- 让每个迭代独立以保证循环可以以任何顺序正确的执行
比如下面这段代码片段,A[i]的值依赖于j的值,j的值又依赖于上一次j的值。这样就导致循环无法并行起来。
1
2
3
4
5
6
int i, j, A[MAX];
j = 5;
for (i = 0; i < MAX; i++) {
j += 2;
A[i] = big(j);
}
将j的计算改造一下,就可以使得当前迭代不再依赖于上一次迭代,就可以并行起来。如下所示:
1
2
3
4
5
6
int i, j, A[MAX];
#pragma omp parallel for
for (i = 0; i < MAX; i++) {
int j = 5 + 2 * (i + 1);
A[i] = big(j);
}
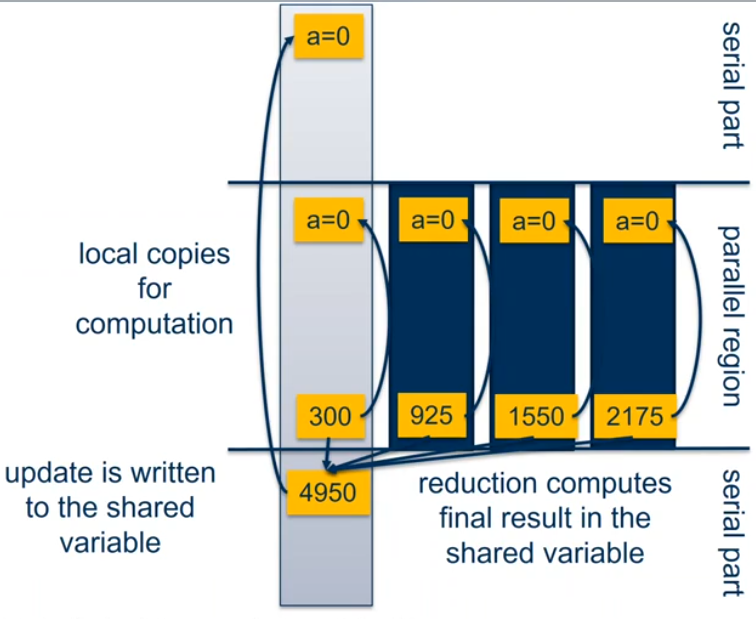
reduction原语
在reduction操作中,运算符应用于列表中的所有变量。这些变量必须是共享的。
reduction(operator:list)结果在相关的
reduction变量中提供。每个列表变量会产生一份本地副本,根据
op的不同初始化成相应的值。对本地副本进行更新。
本地副本
reduce成一个值,然后和原始的全局值组合。- 可能的
reduction操作及初始化值:+ (0),* (1),- (0),& (~0),^ (0),| (0),&& (1),|| (0),min (最大数),max (最小数)
12. 讨论4-Pi程序总结
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void calc_pi_reduction()
{
static long num_steps = 0x20000000;
double step;
double sum = 0.0;
step = 1.0 / (double)num_steps;
double start = omp_get_wtime( );
#pragma omp parallel
#pragma omp for reduction(+:sum)
for (long i = 0; i < num_steps; i++) {
double x = (i + 0.5) * step;
sum += 4.0 / (1.0 + x * x);
}
double pi = sum * step;
double end = omp_get_wtime( );
printf("pi: %.16g in %.16g secs\n", pi, end - start);
}
13. Barriers…和更多Constructs
barrier原语
线程等待,直到当前组的所有线程都达到屏障。
所有worksharing constructs的末尾都包含隐式屏障。
1
2
3
4
5
6
7
#pragma omp parallel
{
int id = omp_get_thread_num();
A[id] = big_cal1(id);
#pragma omp barrier
B[id] = big_cal2(ia, A);
}
14. OpenMP中的锁
Lock方法
omp_init_lock()omp_set_lock()omp_uset_lock()omp_destroy_lock()omp_test_lock()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#pragma omp parallel for
for(i=0; i < NBUCKETS;i++) {
omp_init_lock(&hist_locks[i]);
hist[i] = 0;
}
#pragma omp parallel for
for(i = 0; i < NVALS; i++) {
ival = sample(arr[i]);
omp_set_lock(&hist_locks[ival]);
hist[ival]++;
omp_unset_lock(&hist_locks[ival]);
}
#pragma omp parallel for
for(i=0; i < NBUCKETS;i++) {
omp_destroy_lock(&hist_locks[i]);
}
15. OpenMP的运行时库方法
运行时库方法
omp_set_num_threads()omp_get_num_threads(),在并行域外调用这个接口,返回值是1omp_get_thread_num()omp_get_max_threads()omp_in_parallel()omp_set_dynamic()omp_get_dynamic()omp_num_procs()
16. OpenMP的环境变量
OMP_NUM_THREADSOMP_STACKSIZEOMP_WAIT_POLICY,(ACTIVE or PASSIVE)OMP_PROC_BIND,(TRUE or FALSE)
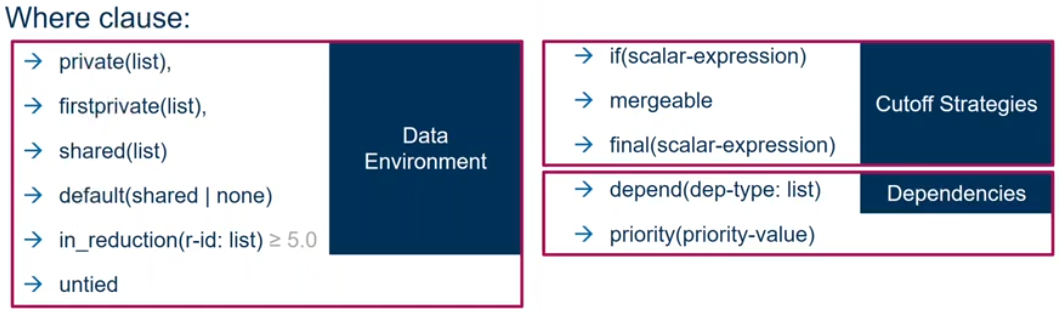
17. 数据作用域
由于OpenMP是基于共享内存的编程模型,所以大部分变量的属性默认是shared,比如static变量、文件作用域的变量。但是并不是一切都是shared,并行域里调用的函数的栈变量是private,语句块里的自动变量是private。基本原则是:Heap is shared, stack is private.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
double A[10];
int main() {
int index[10];
#pragma omp parallel
work(index);
printf("%d\n", index[0]);
}
extern double A[10];
void work(int* index) {
double temp[10];
static int count;
...
}
/*
A, index, count 是shared
temp是private
*/
改变存储属性
sharedprivate1 2 3 4 5 6 7 8
void wrong() { int tmp = 0; #pragma omp parallel for private(tmp) //tmp的私有副本是未初始化的 for(int j = 0; j < 1000; j++) { tmp += j; } printf("%d\n", tmp); // 会打印全局tmp的值0 }
- firstprivate
1 2 3 4 5 6 7
int incr = 0; // incr的私有副本会用全局incr的值0作为初始值,for循环结束后,私有副本会消失 #pragma omp parallel for firstprivate(incr) for(i=0; i <=MAX; i++) { if ((i % 2) == 0) incr++; A[i]=incr; }
- lastprivate
1 2 3 4 5 6 7 8 9 10 11 12
void sq2(int n, double *lastterm) { double x; int i; // 最后一次循环(i=N-1)得到的x的值会传给全局x,进而赋给lastterm指针指向的对象 #pragma omp parallel for lastprivate(x) for(i = 0; i < N; i++) { x = a[i]*a[i] + b[i]*b[i]; b[i] = sqrt(x); } *lastterm = x; }
- default(private/shared/none)
OpenMP中的作用域: 将变量分为shared和private:
- private-list and shared-list on Parallel Region.
- private-list and shared-list on Worksharing constructs.
- General default is shared for Parallel Region, firstprivate for Task.
- Loop control variables on for-constructs are private.
- Non-static variables local to Parallel Regions are private.
private: A new uninitialuized instance is created for the task or each thread executing the construct.firstprivate: Initialization with the value before encountering the constructlastprivate: Value of last loop iteration is written back to Master
- 静态变量是
shared.
全局/静态变量的私有化
全局/静态变量可以通过threadprivate原语被私有化。
- One instance is created for each thread
- before the first parallel region is encountered.
- instance exists until the program ends
- does not work (well) with nested parallel region.
- Based on thread-local storage(TLS)
1 2
static i; #pragma omp threadprivate(i)
18. 讨论5-调试OpenMP程序
下面是错误版本。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include "omp.h"
#include <cstdio>
#define NPOINTS 1000
#define MXITR 1000
struct d_complex {
double r;
double i;
};
struct d_complex c;
int numoutside = 0;
void testpoint()
{
struct d_complex z;
int iter;
double temp;
z = c;
for(iter=0; iter<MXITR; iter++) {
temp = (z.r*z.r)-(z.i*z.i)+c.r;
z.i=z.r*z.i*2+c.i;
z.r=temp;
if((z.r*z.r+z.i*z.i) > 4.0) {
numoutside++;
break;
}
}
}
void MandelBrotArea()
{
int i, j;
double area, error, eps = 1.0e-5;
#pragma omp parallel for default(shared) private(c, eps)
for (i = 0; i < NPOINTS; i++) {
for (j = 0; j < NPOINTS; j++) {
c.r = -2.0 + 2.5*(double)(i) / (double)NPOINTS + eps;
c.i = 1.125*(double)(j) / (double)NPOINTS + eps;
testpoint();
}
}
area = 2.0*2.5*1.125 * (double)(NPOINTS*NPOINTS-numoutside) / (double)(NPOINTS*NPOINTS);
error=area/(double)NPOINTS;
printf("error: %d\n", error);
}
int main(void) {
MandelBrotArea();
return 0;
}
将default设置为none,可以用来调试。
1
2
- #pragma omp parallel for default(shared) private(c, eps)
+ #pragma omp parallel for default(none) private(c, eps)
再进行编译的时候就会error信息:
1
2
3
4
5
6
7
mandelbrot_wrong.cc: In function ‘void MandelBrotArea()’:
mandelbrot_wrong.cc:38:16: error: ‘j’ not specified in enclosing ‘parallel’
for (j = 0; j < NPOINTS; j++) {
~~^~~
mandelbrot_wrong.cc:36:9: error: enclosing ‘parallel’
#pragma omp parallel for default(none) private(c, eps)
^~~
下面是正确的版本。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#define NPOINTS 1000
#define MXITR 1000
struct d_complex {
double r;
double i;
};
struct d_complex c;
int numoutside = 0;
void testpoint(struct d_complex c)
{
struct d_complex z;
int iter;
double temp;
z = c;
for(iter=0; iter<MXITR; iter++) {
temp = (z.r*z.r)-(z.i*z.i)+c.r;
z.i=z.r*z.i*2+c.i;
z.r=temp;
if((z.r*z.r+z.i*z.i) > 4.0) {
#pragma omp atomic
numoutside++;
break;
}
}
}
void MandelBrotArea()
{
int i, j;
double area, error, eps = 1.0e-5;
#pragma omp parallel for default(shared) private(c, j) firstprivate(eps)
for (i = 0; i < NPOINTS; i++) {
for (j = 0; j < NPOINTS; j++) {
c.r = -2.0 + 2.5*(double)(i) / (double)NPOINTS + eps;
c.i = 1.125*(double)(j) / (double)NPOINTS + eps;
testpoint(c);
}
}
area = 2.0*2.5*1.125 * (double)(NPOINTS*NPOINTS-numoutside) / (double)(NPOINTS*NPOINTS);
error=area/(double)NPOINTS;
printf("error: %d\n", error);
}
下面是两个版本之间的差异
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
diff --git a/mandelbrot_wrong.cc b/mandelbrot.cc
index 833155f..e6aadd1 100644
--- a/mandelbrot_wrong.cc
+++ b/mandelbrot.cc
@@ -11,7 +11,7 @@ struct d_complex {
struct d_complex c;
int numoutside = 0;
-void testpoint()
+void testpoint(struct d_complex c)
{
struct d_complex z;
int iter;
@@ -23,6 +23,7 @@ void testpoint()
z.i=z.r*z.i*2+c.i;
z.r=temp;
if((z.r*z.r+z.i*z.i) > 4.0) {
+ #pragma omp atomic
numoutside++;
break;
}
@@ -33,12 +34,12 @@ void MandelBrotArea()
{
int i, j;
double area, error, eps = 1.0e-5;
-#pragma omp parallel for default(shared) private(c, eps)
+#pragma omp parallel for default(shared) private(c, j) firstprivate(eps)
for (i = 0; i < NPOINTS; i++) {
for (j = 0; j < NPOINTS; j++) {
c.r = -2.0 + 2.5*(double)(i) / (double)NPOINTS + eps;
c.i = 1.125*(double)(j) / (double)NPOINTS + eps;
- testpoint();
+ testpoint(c);
}
}
改动最少的计算pi的版本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void calc_pi_reduction()
{
static long num_steps = 0x20000000;
double step;
double sum = 0.0;
step = 1.0 / (double)num_steps;
double start = omp_get_wtime( );
#pragma omp parallel
#pragma omp for reduction(+:sum)
for (long i = 0; i < num_steps; i++) {
double x = (i + 0.5) * step;
sum += 4.0 / (1.0 + x * x);
}
double pi = sum * step;
double end = omp_get_wtime( );
printf("pi: %.16g in %.16g secs\n", pi, end - start);
}
19. 技能训练:链表和OpenMP
到目前为止,介绍了
- To create a team of threads:
#pragma omp parallel - To share work between threads
#pragma omp for#pragma omp single
- To prevent conflicts(data races)
#pragma omp critical#pragma omp atomic#pragma omp barrier#pragma omp master
- Data environment clauses
private(variable_list)firstprivate(variable_list)lastprivate(variable_list)reduction(op:variable_list)
考虑如何将下面的链表遍历代码并行化,
1
2
3
4
5
p = head;
while(p) {
process(p);
p = p->next;
}
20. 讨论6-遍历链表的不同方法
Ugly solution
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
while(p) {
p = p->next;
count++;
}
p = head;
for (int i = 0; i < count; i++) {
parr[i] = p;
p = p->next;
}
#pragma omp parallel
{
#pragma omp for schedule(static, 1)
for (int i = 0; i < count; i++) {
process(parr[i]);
}
}
21. Tasks(Linked List the Easy Way)
Tasks are independent units of work.
1
2
#pragma omp task [clause[[,] clause]...]
{structured-block}
Tasks are composed of:
- code to execute
- data environment
- internal control variables(ICV)
The runtime system decides when tasks are executed.
例子:
1
2
3
4
5
6
7
8
9
10
11
#pragma omp parallel
{
#pragma omp task //每个线程创建一个任务foo()
foo();
#pragma omp barrier
#pragma omp single // 只有一个线程创建任务bar()
{
#pragma omp task
bar();
}
}
taskwait directive
- It’s a stand-alone directive
1
#pragma omp taskwait - wait in the completion of child tasks of the current task; just direct children, not all descendant tasks; includes an implicit task scheduling point(TSP)
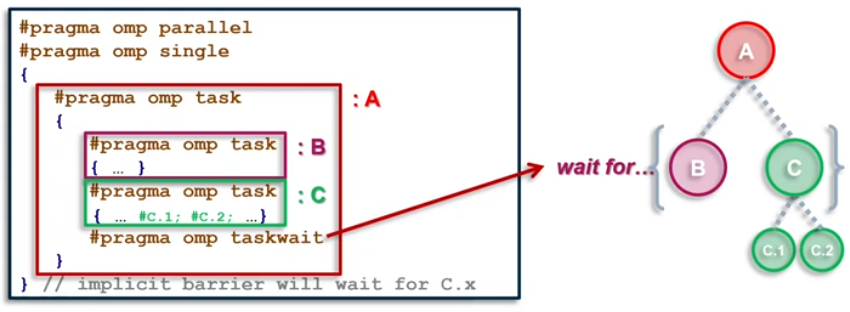
if clause
The if clause of a task construct
- allows to optimize task creation/execution
- reduces parallelism but also reduces the pressure in the runtime’s task pool.
- for “very” fine grain tasks you may need to do your own
if1
#pragma omp task if (expression) - If the expression of the
ifclause evaluates to false- the encountering task is suspended
- the new task is executed immediately
- the parent task resumes when the task finishes
- This is known as undeferred task


Tasking Overheads
Typical overheads in task-based programs are:
- Task Creation: populate task data structure, add task to task queue
- Task execution: retrieve a task from the queue(may including work stealing)
If tasks become too fine-grained, overhead becomes noticeable
- Execution spends a higher relative amount of time in the runtime
- Task execution contributing to runtime becomes significantly smaller
A rough rule of thumb to avoid(visiable) tasking overhead
- OpenMP tasks: 80-100k instructions executed per task
- TBB tasks: 30-50k instructions executed per task
- Other programming models may have another ideal granularity
Tasks vs Threads
Threads do not compose well
- Example: multi-threaded plugin in a multi-threaded application
- Composition usually leads to oversubscription and load imbalance
Task models are inherently composable
- A pool of threads executes all created tasks
- Tasks from different modules can freely mix
Task models make complex algorithms easier to parallelize
- Programmers can think in concurrent pieces of work
- Mapping of concurrent execution to threads handled elsewhere
- Task creation can bu irregular(e.g., recursion, graph traversal)
Sometimes you are better off with threads
Some scenarios are more amenable for traditional threads
- Granularity too coarse for tasking
- Isolation of autonomous agents
Static allocation of parallel work is typically easier with threads
- Controlling allocation of work to cache hierarchly
Graphical User Interface(event thread + worker threads)
Request/response processing, e.g.,
- Web Server
- Database servers
Tasking and Scoping
Data scoping in tasks
Some rules from Parallel Regions apply
- Automatic Storage(local) variables are private
- Static and global variables are shared
Tasking: variables are firstprivate unless shared in the enclosing context
- Only shared attribute is inherited
- Exception: Orphaned Task variables are firstprivate by default
Example
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int a = 1;
void foo() {
int b = 2, c = 3;
#pragma omp parallel private(b)
{
int d = 4;
#pragma omp task
{
int e = 5;
// scope of a: shared, value of a: 1
// scope of b: firstprivate, value of b: 0 or undefined
// scope of c: shared, value of c: 3
// scope of d: firstprivate, value of d: 4
// scope of e: private, value of e: 5
}
}
}

Orphaned Task Variables
- Arguments passed by reference are
firstprivateby default in orphaned task generating constructs, example:
22. 讨论7-理解Tasks
用task实现遍历链表
1
2
3
4
5
6
7
8
9
10
11
12
#pragma omp parallel
{
#pragma omp single
{
node* p = head;
while (p) {
#pragma omp task firstprivate(p);
process(p);
p = p->next;
}
}
}

23. 可怕的东西:内存模型,Atomics,Flush(Pairwise同步)
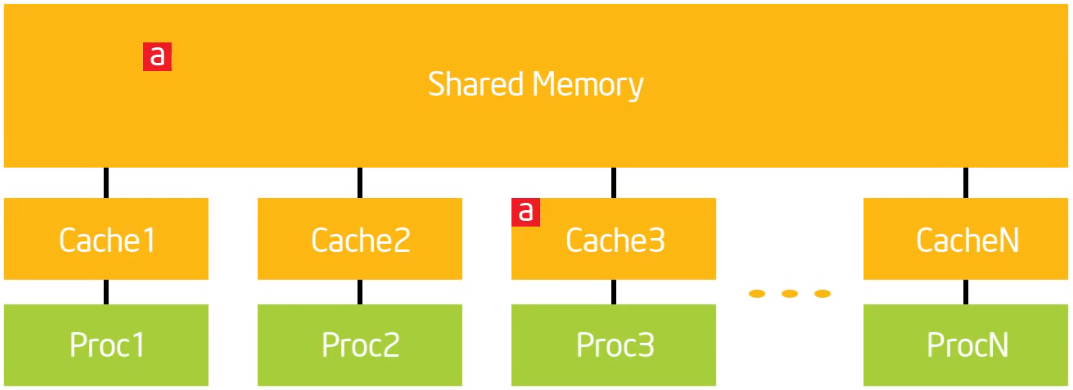
sequential consistency
在一个多核处理器中,操作(R/W/S)是sequential consistency的,如果:
- 对于每个核,它们保持这代码中的顺序
- 其他每个处理器看到它们的总体顺序是相同的
OpenMP defines consistency as a variant of weak consistency.
Can not reorder S ops with R or W ops on the same thread.
Weak consistency guarantees S>>W, S>>R, R>>S, W>>S, S>>S
Flush
Defines a sequence point at which a thread is guaranteed to see a consistent view of memory with respect to the flush set.
The flush set is:
- A list of variables when the
flush(list)construct is used All thread visiable variablesfor a flush construct without an argument list
The action of flush is to guarantee that:
- All R/W ops that overlap the flush set and occur prior to the flush complete before the flush executes.
- All R/W ops that overlap the flush set and occur after the flush don’t execute until after the flush executes.
- Flushes with overlapping flush sets can not be reordered.
A flush operation is implied by OpenMP synchronizations, e.g.
- At entry/exit of parallel regions
- At implicit and explicit barriers
- At entry/exit of critical regions
24. 讨论8-Pairwise同步的陷阱
Pair Wise Synchronization in OpenMP
OpenMP lacks synchronization constructs that work between pairs of threads. When this is needed, you have to build it yourself.
Pair Wise Synchronization:
- use a shared flag variable
- reader spins waiting for the new flag value
- use flushed to force updates to and form memory
一个例子,生产者-消费者模型的例子。
1
2
3
4
5
6
7
8
9
10
11
12
int main()
{
double* A, sum, runtime;
int flag = 0;
A = (double*)malloc(N * sizeof(double));
fill_rand(N, A); // producer: fill an array of data
sum = Sum_arrat(N, A); // consumer: sum the array
return 0;
}
将上述例子用OpenMP并行化,如下所示,这个改法有个极低概率的bug,就是flag = 1;的操作不算原子的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int main()
{
double* A, sum, runtime;
int flag = 0;
A = (double*)malloc(N * sizeof(double));
#pragma omp prallel sections
{
#pragma omp section
{
fill_rand(N, A); // producer: fill an array of data
#pragma omp flush
flag = 1;
#pragma omp flush (flag)
}
#pragma omp section
{
#pragma omp flush (flag)
while (flag == 0) {
#pragma omp flush (flag)
}
#pragma omp flush
sum = Sum_arrat(N, A); // consumer: sum the array
}
}
return 0;
}
atomic
Atomic is expanded to cover the full range of common scenarios where you need to protect a memory operation so it occurs atomically.
1
#pragma omp atomic [read | write | update | capture]
atomic can protect loads
1 2
#pragma omp atomic read v = x;
atomic can protect stores
1 2
#pragma omp atomic write x = expr;
用atomic解决非原子操作问题。代码如下所示。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
int main()
{
double* A, sum, runtime;
int flag = 0, flag_tmp;
A = (double*)malloc(N * sizeof(double));
#pragma omp prallel sections
{
#pragma omp section
{
fill_rand(N, A); // producer: fill an array of data
#pragma omp flush
#pragma omp atomic write
flag = 1;
#pragma omp flush (flag)
}
#pragma omp section
{
while(1) {
#pragma omp flush (flag)
#pragma atomic write
flg_temp = flag;
if (flag_tmp == 1) break;
}
#pragma omp flush
sum = Sum_arrat(N, A); // consumer: sum the array
}
}
return 0;
}
25. 线程私有数据和如何支持库(Pi again)
threadprivate: makes global data private to a thread.
1
2
3
4
5
6
7
8
int counter = 0;
#pragma omp threadprivate(counter) //每个线程都有一个counter变量,并且被初始化为0
int increment_counter()
{
counter++;
return (counter);
}
26. 讨论 9-随机数生成器
蒙特卡洛法计算pi值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <random>
static long num_trails = 10000;
void calc_pi_montacalo()
{
long i;
long Ncircle = 0;
double pi, x, y;
double r = 1.0;
std::random_device rd;
std::mt19937 rng(rd());
std::uniform_real_distribution<> dist(-1.0, 1.0);
#pragma omp parallel for private(x, y) reduction(+:Ncircle)
for(i = 0; i < num_trails; i++) {
x = dist(rng);
y = dist(rng);
if ((x * x + y * y) <= r * r) {
Ncircle++;
}
}
pi = 4.0 * ((double)Ncircle / (double)num_trails);
printf("\n%d trails, pi is %f\n", num_trails, pi);
}
线性同余法
Linear Congruential Generator(LCG): easy to write, cheap to compute, portable, OK quality.
1
2
random_next = (MULTIPLIER* random_last + ADDEND) % PMOD;
random_last = random_next;
If you pick the multiplier and addend correctly, LCG has a period of PMOD.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
/* simple single thread version */
static long MULTIPLIER = 1366;
static long ADDEND = 150889;
static long PMOD = 714025;
long random_last = 0;
double random()
{
long random_next;
random_next = (MULTIPLIER* random_last + ADDEND) % PMOD;
random_last = random_next;
return ((double)random_next / (double)PMOD);
}
27. 概括
新手并行程序员与专家并行程序员之间的区别是专家have a collection of these fundamental design patterns in their minds.
SPMD
Single Program Multiple Data: Run the same program on P processing elements where P can be arbitrarily large.
Use the rank - an ID ranging from 0 to (P-1) - to select between a set of tasks and to manage any shared data structures.
例子:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include "omp.h"
void main()
{
int i, step;
double pi = 0.0, sum = 0.0;
step = 1.0 / (double)num_steps;
#pragma omp parallel firstprivate(sum) private(x, i)
{
int id = omp_get_threads_num();
int numprocs = omp_get_num_threads();
int step1 = id * num_steps / numprocs;
int stepN = (id+1) * num_steps / numprocs;
if (id == numprocs - 1) {
stepN = num_steps;
}
for (ri = step1; i < stepN; i++) {
x = (i+0.5)*step;
sum += 4.0/(1.0+x*x);
}
#pragma omp critical
pi += sum*step;
}
}
Loop Parallelism
Collections of tasks are defined as iterations of one or more loops.
Loop iterations are divided between a collection of processing elements to compute tasks in parallel.
例子:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void calc_pi_reduction()
{
static long num_steps = 0x20000000;
double step;
double sum = 0.0;
step = 1.0 / (double)num_steps;
double start = omp_get_wtime( );
#pragma omp parallel
#pragma omp for reduction(+:sum)
for (long i = 0; i < num_steps; i++) {
double x = (i + 0.5) * step;
sum += 4.0 / (1.0 + x * x);
}
double pi = sum * step;
double end = omp_get_wtime( );
printf("pi: %.16g in %.16g secs\n", pi, end - start);
}
分治Pattern
当问题存在分解成子问题的方法和将子问题的解重新组合为全局解的方法时使用。
定义一个分解操作。
持续分解直到子问题小到可以直接求解。
将子问题的解组合起来解决原始的全局问题。
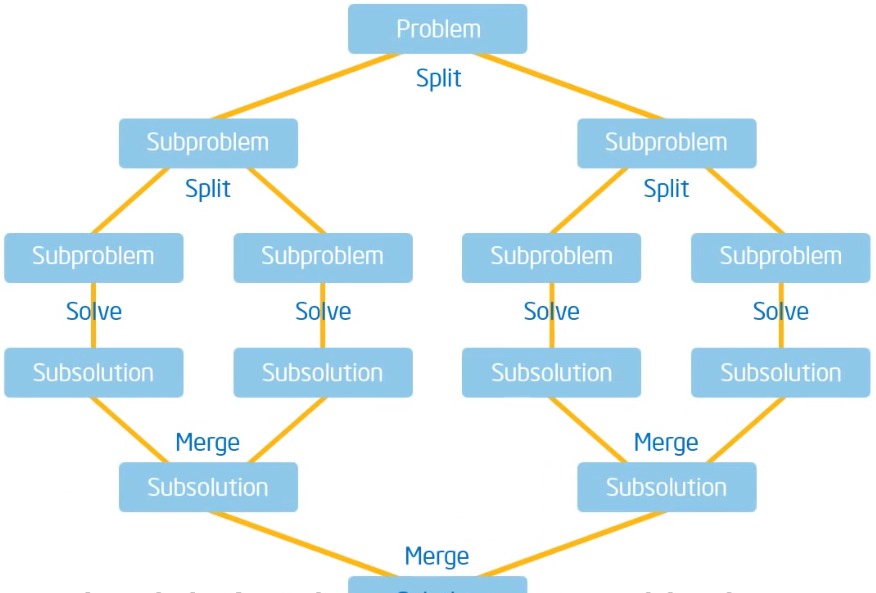
例子:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include "omp.h"
static long num_steps = 100000000;
#define MIN_BLK 10000000
double pi_comp(int Nstart, int Nfinish, double step)
{
int i, iblk;
double x, sum = 0.0, sum1, sum2;
if(Nfinish - Nstart < MIN_BLK) {
for(i = Nstart; i < Nfinish; i++) {
x = (i+0.5)*step;
sum += 4.0/(1.0+x*x);
}
} else {
iblk = Nfinish - Nstart;
#pragma omp task shared(sum1)
sum1 = pi_comp(Nstart, Nfinish - iblk/2, step);
#pragma omp task shared(sum2)
sum2 = pi_comp(Nfinish - iblk/2, Nfinish, step);
#pragma omp taskwait
sum = sum1 + sum2;
}
return sum;
}
int main()
{
int i;
double step, pi, sum;
step = 1.0 / (double)num_steps;
#pragma omp parallel
{
#pragma omp single
sum = pi_comp(0, num_steps, step);
}
pi = step * sum;
return 0;
}
推荐的参考书
“Using OpenMP-portable shared memory parallel programing”
“Patterns for Parallel Programing”
“Introduction to Concurrency in Programming Languages”
“The Art of Concurrency”

